Fatoração
Fatorar uma expressão algébrica significa escrevê-la na forma de um produto de expressões mais simples.
Casos de fatoração:
FATOR COMUM
ax + bx + cx = x . (a + b + c)
O fator comum é x.
12x3 - 6x2 + 3x = 3x . (4x2 - 2x + 1)
O fator comum é 3x.
AGRUPAMENTO
ax + ay + bx + by
Agrupar os termos de modo que em cada grupo haja um fator comum.
(ax + ay) + (bx + by)
Colocar em evidência o fator comum de cada grupo
a(x + y) + b(x + y)
Colocar o fator comum (x + y) em evidência
(x + y) . (a + b) Þ Este produto é a forma fatorada da expressão dada
DIFERENÇA DE DOIS QUADRADOS
A expressão a2 - b2 representa a diferença de dois quadrados e sua forma fatorada é :
(a + b) (a - b)
Ex: x2 - 36 = (x + 6) (x - 6)
TRINÔMIO QUADRADO PERFEITO
a2 + 2ab + b2
Um trinômio é quadrado perfeito quando :
- dois de seus termos são quadrados perfeitos (a2 e b2 )
- o outro termo é igual ao dobro do produto das raízes dos quadrados perfeitos (2ab)
a2 + 2ab + b2 = (a + b)2
Ex: x2 + 6x + 9 = (x + 3)2
a2 - 2ab + b2 = (a - b)2
Ex: x2 - 6x + 9 = (x - 3)2
TRINÔMIO DO 2O GRAU
Trinômio do tipo x2 + Sx + P
Devemos procurar dois números a e b que tenham soma S e produto P.
x2 + Sx + P = (x + a) (x + b)
Ex: x2 + 5x + 6 = (x + 2) (x + 3)
x2 + 2x - 8 = (x + 4) (x - 2)
x2 - 5x + 6 = (x - 2) (x - 3)
x2 - 2x - 8 = (x - 4) (x + 2)
SOMA DE DOIS CUBOS
A expressão a3 + b3 representa a soma de dois cubos.
Sua forma fatorada é :
(a + b) (a2 - ab + b2)
Ex: x3 + 8 = (x + 2) (x2 - 2x + 4)
DIFERENÇA DE DOIS CUBOS
A expressão a3 - b3 representa a diferença de dois cubos.
Sua forma fatorada é :
(a - b) (a2 + ab + b2)
Ex: x3 - 27 = (x - 3) (x2 + 3x + 9)
Fonte: www.sosmatematica.com
Quando a gente fatora uma expressão, na verdade, a gente esta transformando
esta expressão em fatores de uma multiplicação. Para conseguirmos isto utilizamos
algumas técnicas tais como:
1. Fator comum em evidência
2. Agrupamento de termos semelhantes
3. Diferença de dois quadrados
4. Trinômio quadrado perfeito.
5. Trinômio do segundo grau.
Achou alguns nomes acima complicados ? Não se preocupe! Vamos ver, a seguir,
um exemplo de cada uma destas técnicas utilizadas para a fatoração de uma expressão.
1. Fator comum em evidência: 12x2 + 4x3 - 8x4
Nesta técnica a gente verifica cada um dos termos, procurando ver se os
coeficientes (o que fica na na frente das variáveis x, y etc), podem ser
divididos por um certo número. Neste caso 12, +4, -8 podem ser divididos
por 4. Então, colocamos o número 4 em evidência, ou seja, antes de um
parênteses, dividimos cada um dos coeficientes por 4 e escrevemos o
resultado no lugar o próprio coeficiente. Veja:
12x2 + 4x3 - 8x4
4 (3x2 + 1x3 - 2x4). Observe que se multiplicarmos o 4 pelos novos coeficientes
3, 1 e -2 iremos ter de volta os coeficientes originais 12, 4 e -8.
Nós escolhemos o 4 para dividir os coeficientes porquê ele é o maior número que
pode dividir cada um dos coeficientes. Não poderíamos ter escolhido, o 8, por exemplo, pois ele é maior que o 4 e não daria para fazer divisão exata, ok ?
1. Fator comum em evidência (Continuação) :
12x2 + 4x3 - 8x4 = 4 (3x2 + 1x3 - 2x4)
Agora precisamos verificar se podemos dividir cada um dos termos que estão dentro
dos parênteses, por um mesmo fator literal (que contém letra). Neste caso podemos
notar que o fator x2 serve para dividir cada uma dos termos da expressão.
Desta forma, escrevemos o x2 antes dos parênteses, ao lado do número 4, e dividimos
cada um dos termos por ele. Veja como fica:
4x2 (3 + 1x - 2x2)
Lembrete: x4 / x3 = x (Divisão de
de mesma base: repete a base e subtrai
os expoentes.
Observe que se multiplicarmos o 4x2 pelos termos dentro dos parênteses iremos obter
a expressão original 12x2 + 4x3 - 8x4. Desta forma, através da técnica de por o fator
comum em evidência, da fatoração, concluímos que 12x2 + 4x3 - 8x4 = 4x2 (3 + x - 2x2).
2. Agrupamento dos termos semelhantes: xy + xz + ay + az
Esta técnica de fatoração consiste em juntar os termos que são iguais e tentar
colocar algo em evidência como fizemos nos exemplos anteriores. Vejamos:
vamos fatorar xy + xz + ay + az.
Primeiro a gente tenta ver os termos que têm partes iguais. Neste caso o xy e xz
têm algo igual: a letra x e, portanto, a gente pode por o x em evidência, que nem fizemos
no exemplo anterior, e o y e o z dentro dos parênteses. Veja:xy + xz = x(y +z).
Então até agora estamos assim: xy + xz + ay + az = x(y +z) + ay + az.
Segundo, a gente nota também que o ay e o az têm parte comum: a letra a. Então
fazemos a mesma coisa: ay + az = a (y + z). Desta forma a expressão original
xy + xz + ay + az é igual a x(y +z) + a (y + z). Finalmente notamos que (y + z) é
comum a x e a, então fazemos novamente a mesma coisa. Colocamos o (y + z) em
evidência e o x e o a dentro dos parênteses. Veja: (y + z) (x + a). Observe que se
fizermos esta multiplicação obteremos a expressão original pois (y + z) (x + a) = xy + xz + ay + az.
3. Diferença de dois quadrados: x2 - y2
Esta técnica consiste em notar que a expressão, ou parte dela, nada mais é que
o resultado de um produto notável do tipo produto da soma pela diferença.
Neste caso, percebemos que a expressão x2 - y2 é o resultado do desenvolvimento
do produto notável (x + y )( x - y ).
Então ao invés de escrevermos x2 - y2 simplesmente escrevemos os fatores
(x + y )( x - y ) pois x2 - y2 = (x + y )( x - y ).
4. Trinômio quadrado perfeito: x2 +2xy + y2
Assim como o caso anterior, esta técnica consiste em notar que a expressão, ou parte dela,
nada mais é que o resultado de um produto notável do tipo a mais b ao quadrado.
Neste caso, percebemos que a expressão x2 +2xy + y2 é o resultado do desenvolvimento
do produto notável (x + y )2.
Então ao invés de escrevermos x2 +2xy + y2 simplesmente escrevemos (x + y )2 pois
x2 +2xy + y2 = (x + y )2.
5. Trinômio do segundo grau: x2 +7x +12
Nesta última técnica, procuramos identificar na expressão, um trinômio do
segundo grau. No exemplo acima, se observarmos atentamente, notaremos
que -7 é a soma das raízes da equação e 12 é o produto destas raízes.
Lembrete: Numa equação do segundo grau a soma das raízes é dada por
-b/a e o produto é dado por c/a, sabendo-se que neste caso a=1, b=7,
e c=12, fica fácil perceber que a Soma é -7/1=-7 e o Produto é 12/1 = 12.
Agora que sabemos a soma (-7) e o produto (12) calculamos por tentativa,
dois número cuja soma seja -7 e o produto seja 12...é claro que os números
são -3 e -4 pois (-3) + (-4) = -7 e (-3).(-4) = 12. Daí escrevemos os fatores
(x - primeira raiz ).(x - segunda raiz) = (x - (-3).(x - (-4) = (x + 3) (x + 4).
Note que efetuando a multiplicação dos fatores (x + 3) (x + 4) obteremos
a expressão original x2 +7x +12.
Fonte: www.interaula.com
Fatorar é transformar equações algébricas em produtos de duas ou mais expressões, chamadas fatores.
Ex: ax + ay = a.(x+y)
Existem vários casos de fatoração como:
1) Fator Comum em evidência
Quando os termos apresentam fatores comuns
Observe o polinômio:
ax + ay » Ambos os termos apresentam o fator a em evidência.
Assim: ax + ay = a.(x+y)
Forma fatorada
Exs : Fatore:
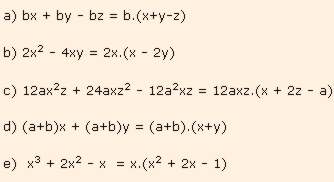
2) Fatoração por agrupamento
Consiste em aplicar duas vezes o caso do fator comum em alguns polinômios especiais.
Como por exemplo:
ax + ay + bx + by
Os dois primeiros termos possuem em comum o fator a , os dois últimos termos possuem em comum o fator b. Colocando esses termos em evidência:
a.(x+y) + b.(x+y)
Este novo polinômio possui o termo (x+y) em comum. Assim colocando-o em evidência:
(x+y).(a+b)
Ou seja: ax + ay + bx + by = (x+y).(a+b)
Exs: Fatore:
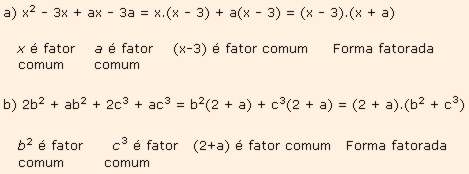
3) Fatoração por diferença de quadrados:
Consiste em transformar as expressões em produtos da soma pela diferença, simplesmente extraindo a raiz quadrada de cada quadrado
Assim: x2 - 9 = (x + 3).(x - 3)
Exs: Fatore:
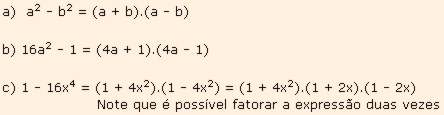
4) Fatoração do trinômio quadrado perfeito:
O trinômio que se obtém quando se eleva um binômio ao quadrado chama-se trinômio quadrado perfeito.
Por exemplo, os trinômios (a2 + 2ab + b2 ) e ( a2 - 2ab + b2 ) são quadrados perfeitos porque são obtidos quando se eleva (a+b) e (a-b) ao quadrado, respectivamente.
(a + b)2 = a2 + 2ab + b2 (a - b)2 = a2 - 2ab + b2


Fonte: www.vestibular1.com.br
- Sistemas Lineares E Determinantes - História
Seki KowaNa matemática ocidental antiga são poucas as aparições de sistemas de equações lineares. No Oriente, contudo, o assunto mereceu atenção bem maior. Com seu gosto especial por diagramas, os chineses representavam os sistemas lineares por...
- Equação De 1º Grau
Introdução às equações de primeiro grau Para resolver um problema matemático, quase sempre devemos transformar uma sentença apresentada com palavras em uma sentença que esteja escrita em linguagem matemática. Esta é a parte mais importante e...
- Frações Decimais
O papel das frações e números Decimais Esta página trata do estudo de frações e números decimais, bem como seus fatos históricos, propriedades, operações e aplicações. As frações decimais e números decimais possuem notória importância...
- Divisão
Divisão é a operação inversa da multiplicação e está ligada à ação de repartir em partes iguais. Para indicar a divisão usaremos o sinal: ou ÷ (dividido por) Exemplo: Quando a divisão de um número por outro é exata, dizemos que o primeiro...
- Critérios De Divisibilidade
Sobre a divisibilidade Em algumas situações precisamos apenas saber se um número natural é divisível por outro número natural, sem a necessidade de obter o resultado da divisão. Neste caso utilizamos as regras conhecidas como critérios de divisibilidade....
