Divisão
Divisão é a operação inversa da multiplicação e está ligada à ação de repartir em partes iguais.
Para indicar a divisão usaremos o sinal: ou ÷ (dividido por)
Exemplo:
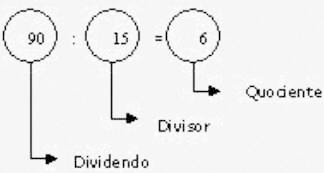
Quando a divisão de um número por outro é exata, dizemos que o primeiro é múltiplo do segundo ou que o primeiro é divisível pelo segundo.
Exemplo: 12 ÷ 2 = 6 (Então 12 é múltiplo de 6 ou 12 é divisível por 6)
A divisão de números naturais também é indicada com um traço horizontal.
Exemplo: 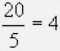
O quociente de números naturais nem sempre é um número natural.
(6 ÷ 5) não é um número natural
A divisão de números naturais não é comutativa.
6 : 3 é diferente de 3 : 6
A divisão de números naturais não é associativa.
(8 : 4) : 2 é diferente de 8 : (4 : 2)
O número 1 não é elemento neutro da divisão de números naturais.
2 ÷ 1 é diferente de 1 ÷ 2
Em uma divisão o divisor não pode ser zero.
Na divisão de zero por um número natural não-nulo, o resultado é sempre zero.
Fonte: www.exatas.net
Divisão de Números Naturais
Dados dois números naturais, às vezes necessitamos saber quantas vezes o segundo está contido no primeiro. O primeiro número que é o maior é denominado dividendo e o outro número que é menor é o divisor. O resultado da divisão é chamado quociente. Se multiplicarmos o divisor pelo quociente obteremos o dividendo.
No conjunto dos números naturais, a divisão não é fechada, pois nem sempre é possível dividir um número natural por outro número natural e na ocorrência disto a divisão não é exata.
Relações essenciais numa divisão de números naturais
1) Em uma divisão exata de números naturais, o divisor deve ser menor do que o dividendo.
35 : 7 = 5
2) Em uma divisão exata de números naturais, o dividendo é o produto do divisor pelo quociente.
35 = 5 x 7
3) A divisão de um número natural n por zero não é possível pois, se admitíssemos que o quociente fosse q, então poderíamos escrever:
n ÷ 0 = q
e isto significaria que:
n = 0 x q = 0
o que não é correto! Assim, a divisão de n por 0 não tem sentido ou ainda é dita impossível.
Fonte: pessoal.sercomtel.com.br
Divisão
Divisão é a operação que permite separar um número em várias partes. Ela é indicada pelos sinais / ou : (dois pontos).
Veja este exemplo:
Paulo tem oito biscoitos e quer dividi-los entre os dois filhos:
Podemos representar isso assim:
Propriedade Fundamental da Divisão
Exata - o quociente é o número que, multiplicado pelo divisor, é igual ao dividendo:
8 : 2 = 4 ou 4 x 2 = 8
A divisão pode ser: exata (como no caso acima) ou com resto.
Divisão com Resto
Nem sempre a divisão é exata.
Vamos ver um exemplo:
Observações:
a) para que a divisão seja realizada, é preciso que o dividendo seja maior que o divisor ou igual a ele:
6 : 3 = 2
6 : 6 = 1
8 : 9 ---- não é possível realizar a divisão
b) não existe divisão por zero.
Divisibilidade
Observe estas divisões de números naturais:
Como você vê, em algumas o resto é igual a zero, isto é, a divisão é exata.
Quando isso acontece dizemos que o dividendo é divisível pelo divisor:
48 é divisível por 4 e 63 é divisível por 3.
Divisibilidade de alguns números - você pode saber se um número é divisível por 2, por 3, por 4, por 5, por 6 ou por 9 sem efetuar a divisão.
Basta saber que:
um número é divisível por 2 quando é par, como 246
um número é divisível por 3 quando a soma dos seus algarismos é divisível por 3, como 162
um número acima de 99 é divisível por 4 quando os dois últimos algarismos formam um número divisível por 4, como 228
um número é divisível por 5 quando seu numeral apresenta, na ordem das unidades, o algarismo 0 ou o 5, ou seja, - quando termina em 0 ou 5, como 300 e 85
um número é divisível por 6 quando é divisível por 2 e por 3
um número é divisível por 9.
Números Primos
Todo número natural é divisível por 1 e por ele mesmo, porém alguns números, como já vimos, são divisíveis por outros números, alem desses dois:
1 é divisível por 1
2 é divisível por 1 e por 2
3 é divisível por 1 e por 3
4 é divisível por 1, por 2 e por 4
5 é divisível por 1 e por 5
6 é divisível por 1, por 2, por 3 e por 6
7 é divisível por 1 e por 7
8 é divisível por 1, por 2, por 4 e por 8
9 é divisível por 1, por 3 e por 9
Números primos são aqueles que só são divisíveis por dois números: por 1 e por ele mesmo.
Os números que são divisíveis por mais de dois números distintos, chamam-se números compostos.
Observação: o número 1 não é primo nem composto, é o único número divisível apenas por um número, ele mesmo.
Para saber se um número é primo, é preciso descobrir se ele é divisível por um dos números primos.
Ao efetuar a divisão o quociente deve ser menor ou igual ao divisor:
Tabela dos Números Primos de 1 a 50
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Múltiplos
Múltiplo de a é todo resultado da multiplicação de um número natural por a.
Veja um exemplo:
4 . 6 = 24, portanto 24 é um múltiplo de 6 ou 4 .
a = 24, portanto 24 é um múltiplo de a.
Para obter todos os múltiplos de 6, você deve multiplicar 6 pelos números naturais:
6 . 0 = 0 6 . 1 = 6 6 . 2 = 12 6 . 3 = 18
6 . 4 = 24 6 . 5 = 30 6 . 6 = 36 6 . 7 = 42
6 . 8 = 48 6 . 9 = 54
OU: 6+6=12+6=18+6=24+6=30+6=36+6=42+6=48+6=54
Decomposição em Fatores Primos
Decompor um número natural em fatores primos é escrever esse número na forma de uma multiplicação em que todos os fatores são números primos.
Observe as várias maneiras de se decompor um número em produto:
20 = 1.2 20 = 2 .10 20 = 4 . 5 20 = 1 . 1 . 20 20 = 1 . 2 . 10
20 = 1 . 4 . 5 20 = 2 . 2 . 5 20 = 1 . 1 . 2 . 10 20 = 1 . 1 . 2 . 2 . 5
Você pode notar que em um dos casos todos os fatores são números primos:
20 = 2 . 2 . 5
O número 20 pode ser decomposto em um produto de números primos. A mesma coisa ocorre com todos os números compostos não nulos.
Lembre-se: todo número natural maior do que 1 ou é primo ou pode ser decomposto em um produto de fatores primos.
Divisores de um Número
Um número natural não nulo b é divisor do número natural a quando a é divisível por b (sendo o resto 0):
4 é divisor de 12 porque 12 é divisível por 4
8 é divisor de 32 porque 32 é divisível por 8
Observação: 1 é divisor de qualquer número natural.
Fonte: www.vestibular1.com.br
Divisão
Maria corta o pão em fatias para o jantar.
Ela calcula: "Somos cinco - eu, meu marido e meus três filhos; seis fatias para cada um é o suficiente. 6 x 5 = 30 fatias".
Na mesa, cada um faz o pensamento inverso ao da mãe: "Uma, duas, três ... são trinta fatias; somos cinco; trinta fatias divididas para cinco pessoas... quer dizer que cada um poderá comer seis fatias".
A sentença matemática que expressa o corte do pão é: 6 x 5 = 30
Na mesa ocorre a inversão: as 30 fatias são divididas (:) entre 5 pessoas resultando ( = ) 6 para cada um.
O verbo dividir em matemática é representado pelo sinal: (lê-se dividido por) e o resultado (o quociente) pelo sinal = (lê-se igual).
Temos assim a sentença matemática:
30 : 5 = 6
A mãe da família pensou o contrário: 30 fatias foram cortadas para que cada pessoa podesse comer 6.
30 : 5 = 6
Partes da divisão
O número que representa o total que vai ser dividido (ou repartido igualmente) chama-se dividendo.
O número que representa a quantidade de partes em que o total vai ser repartido chama-se divisor.
E o seu resultado é chamado de quociente.

Quando usar a divisão?
Veja em que situações você pode usar essa operação.
Você precisa saber isso para resolver os probleminhas de matemática:
Repartição igualitária:
Quatro agricultores formaram uma pequena cooperativa, conseguindo arrecadar R$ 2.540,00 na colheita de milho. Quanto cada um vai receber?
Esse é um problema típico de divisão: ao dividir 2.540 reais para 4 pessoas, pensa-se sempre em quantias iguais para cada um dos agricultores.
A divisão é uma inversão: ela desmancha a operação multiplicação.
Queremos saber qual parte cada um deve receber para que ao juntar as 4 partes (multiplicarmos por 4), obtenha-se o total arrecadado pela venda da colheita (2540).
? x 4 = 2540
Essa pergunta é resolvida pela divisão 2540 : 4 = ?
Previsão:
Um remédio é vendido em cartelas com 48 comprimidos. O médico receitou a José 3 comprimidos ao dia. Quantos dias de tratamento José conseguirá comprando 1 só cartela?
Novamente, queremos saber quantas vezes (quantos dias) ele pode tomar 3 comprimidos até completar os 48 comprimidos de uma cartela.
3 x ? = 48
Esta pergunta é resolvida através de uma divisão 48 : 3 = ?
Roberto P. Moisés
Fonte: www.matematicosufmt.com
É o ato de dividir ou fragmentar algo. É a operação na matemática em que se procura achar quantas vezes um número contém em outro ou mesmo pode ser definido como parte de um todo que se dividiu.
À divisão dá o nome de operação e o resultado é chamado de Quociente.
1) A divisão exata
Veja: 8 : 4 é igual a 2, onde 8 é o dividendo, 2 é o quociente, 4 é o divisor, 0 é o resto
A prova do resultado é: 2 x 4 + 0 = 8
Propriedades da divisão exata
Pode-se afirmar que a divisão exata tem somente uma propriedade.
Observe este exemplo: (10 + 6) : 2 = 16 :2 = 8
(10+6):2 = 10:2 + 6 :2 = 8
O quociente não sofreu alteração alguma permanecendo o mesmo 8. Chamamos então esta propriedade de distributiva da divisão exata válida somente para direita, com relação às operações de adição e subtração.
Um dos mandamentos da matemática é JAMAIS DIVIDA POR ZERO. Isto significa dizer que em uma operação o divisor tem que ser maior do que zero.
2) A divisão não-exata
Observe este exemplo: 9 : 4 é igual a resultado 2, com resto 1, onde 9 é dividendo, 4 é o divisor, 2 é o quociente e 1 é o resto.
A prova do resultado é: 2 x 4 + 1 = 9
De um modo geral na divisão :
Operação divisão exata: D:d = q > d.q = D, onde D = dividendo, d = divisor, q = quociente e o resto é subentendido ?igual a zero?.
Operação divisão não-exata: D = d.q + r, onde D = dividendo, d = divisor, q = quociente, r é o resto.
Fonte: www.juliobattisti.com.br
Na sua forma mais simples a divisão é repartir uma quantidade finita em quantidades iguais.
Divisão é a operação matemática que determina a quantidade de vezes que um número (divisor) está contido dentro de outro número (dividendo). A divisão é a operação inversa da multiplicação.
De um ponto de vista informal, divisão é o ato de dividir, repartir, separar as partes de um todo.
Propriedades
Divisor neutro: Qualquer número dividido por 1 (um) terá como quociente o próprio número dividido.
Anulação: Qualquer número dividido por 8 (infinito) ou -8 (menos infinito) será sempre zero.
Indeterminação: As divisões 0 ÷ 0 e 8 ÷ 8 não têm um quociente determinado; qualquer número pode ser usado como solução.
Divisão por zero: O resultado de uma divisão de um número não-nulo por 0 tende ao infinito. O resultado de 0 dividido por 0 é indeterminado; o resto de uma divisão nunca pode ser um número maior ou igual ao divisor.
A divisão é a única das quatro operações fundamentais que não tem a propriedade de fechamento. Nem sempre um número real pode ser dividido por outro número real, pois nenhum número pode ser dividido por zero.
Fonte: pt.wikiversity.org
O que é um dividendo e um divisor?
Quando a maioria das pessoas pensam sobre dividendos, elas pensam sobre os pagamentos feitos por uma empresa para seus donos. Quando elas pensam sobre divisor, elas acham que é algo que separa as pessoas e/ou objetos. Entretanto, quanto utilizados juntos, "divisor" e "dividendo" estão relacionados à matemática, em específico, sobre as questões de divisão.
Dividendo
Em um problema de divisão, o número que está sendo dividido é o dividendo. Em um problema de divisão padrão, o dividendo aparecerá do lado esquerdo. Por exemplo, no problema 30/5=6, "30" é o dividendo. Caso o problema esteja escrito no formato de uma fração, o dividendo é o numerador, ou o número no topo da fração.
Divisor
O divisor é o número pelo qual o dividendo está sendo dividido na operação matemática. Em um problema de divisão comum, o divisor irá aparecer do lado direito do sinal da divisão. Por exemplo, na operação, 30/5=6 "5" é o divisor. Caso o problema seja uma fração, o divisor é o denominador, ou o número da parte de baixo da fração.
Quociente
O quociente é a solução do problema de divisão. Ele irá aparecer do lado direito do sinal de igual (=) num problema de divisão padrão. Por exemplo, na operação matemática 30/5=6, "6" é o quociente. Da mesma forma, quando o problema é escrito na forma de fração, o quociente também irá aparecer ao lado direito do sinal de igual.
Fórmulas
Os problemas de divisão podem ser escritos das seguintes formas: "Dividendo / Divisor = Quociente" ou "Dividendo ÷ Divisor = Quociente".
Como a multiplicação é o inverso da divisão, você pode ler a operação da seguinte forma: "Quociente x Divisor = Dividendo."
Modos alternativos de divisão
O "dividendo" pode se referir aos pagamentos das empresas a seus acionistas. A maioria das empresas que pagam dividendos fazem isso quatro vezes ao ano. Entretanto, às vezes, as empresas pagam por um dividendo especial, o que ocorre uma única vez. Esses dividendos podem ser pagos em dinheiro, propriedades ou ações extras das ações da empresa.
Fonte: www.ehow.com.br
Esta operação é utilizada para que possamos dividir uma determinada quantidade em partes iguais.
Exemplo:
Eu possuo dez laranjas e quero distribuí-las igualmente entre meus dois amigos, cada um dos meus amigos ficara com cinco laranjas, ou:
10 : 2 = 5
Elementos de uma divisão:
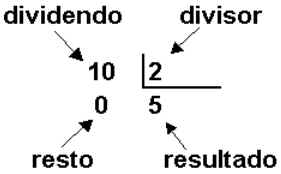
Divisão Exata:
Uma divisão é exata quando o resto é igual a zero.
Divisão Não Exata:
Uma divisão não é exata quando o resto é diferente de zero.
Fonte: www.webquestbrasil.org
- 129 - A ProvÍncia De Santa Catarina E Suas Novas DivisÕes JurÍdicas
129 - A PROVÍNCIA DE SANTA CATARINA E SUAS NOVAS DIVISÕES JURÍDICAS A Província de Santa Catarinacom o tempo foi se reestruturando, no ano de 1847 com a Lei nº 411 de 16 de abril, a qual veio dar nova divisão...
- Origem Dos Sinais
Adição ( + ) e subtração ( - ) O emprego regular do sinal + ( mais ) aparece na Aritmética Comercial de João Widman d'Eger publicada em Leipzig em 1489. Entretanto, representavam não à adição ou à subtração ou aos números positivos...
- Cidade De Assunção - Capital Do Paraguai
Assunção: capital do Paraguai DADOS E INFORMAÇÕES IMPORTANTES: Bandeira da cidade de Assunção País que Pertence: Paraguai Nome Oficial: Nossa Senhora Santa Maria da Assunção Data de Fundação: 15 de agosto de 1537 Gentílico:...
- Frações Decimais
O papel das frações e números Decimais Esta página trata do estudo de frações e números decimais, bem como seus fatos históricos, propriedades, operações e aplicações. As frações decimais e números decimais possuem notória importância...
- Poema Em Homenagem Ao MaciÇo De BaturitÉ/cearÁ
POEMA COMUNHÃO DA SERRA, De José Quintino da Cunha (1875-1943) Ontem, à noite, eu vi a minha...
