Equação do 2º grau
Denomina-se equação do segundo grau, toda a equação do tipo ax²+bx+c, com coeficientes numéricos a.b e c com .
Exemplos:
Classificação
- Incompletas: Se um dos coeficientes ( b ou c ) for nulo, temos uma equação do 2º grau incompleta.
1º caso: b=0
Considere a equação do 2º grau incompleta
x²-9=0 » x²=9 » x=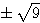 
» x= 
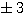
2º caso: c=0
Considere a equação do 2º grau incompleta:
x²-9x=0 » Basta fatorar o fator comum x
x(x-9)=0 » x=0,9
3º caso: b=c=0
2x²=0 » x=0
Resolução de equações do 2º grau:
A resolução de equações do 2º grau incompletas já foi explicada acima, vamos agora resolver equações do 2º grau completas, ou seja, do tipo ax²+bx+c=0 com a, b e c diferentes de zero.
- Uma equação do 2º grau pode ter até 2 raízes reais, que podem ser determinadas pela fórmula de Bháskara.
Como Bháskara chegou até a fórmula de resolução de equações do 2º grau?
Considerando a equação: ax²+bx+c=0, vamos determinar a fórmula de Bháskara:
Multiplicamos os dois membros por 4a:
4a²x²+4abx+4ac=0
4a²x²+4abx=-4ac
Somamos b² aos dois membros:
4a²x²+4abx+b²=b²-4ac
Fatoramos o lado esquerdo e chamamos de 
(delta) b²-4ac:
(2ax+b)²=
2ax+b=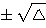 
2ax=-b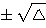
Logo:
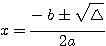ou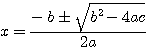 
Fórmula de Bháskara
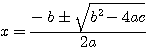
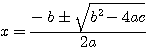
Utilizando a fórmula de Bháskara, vamos resolver alguns exercícios:
1) 3x²-7x+2=0
a=3, b=-7 e c=2
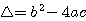= (-7)²-4.3.2 = 49-24 = 25
Substituindo na fórmula:
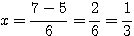
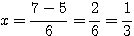
Logo, o conjunto verdade ou solução da equação é:
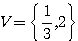
2) -x²+4x-4=0
a=-1, b=4 e c=-4
= 4²-4.-1.-4 = 16-16 = 0
Substituindo na fórmula de Bháskara:
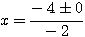» x=2
- Neste caso, tivemos uma equação do 2º grau com duas raízes reais e iguais. ( )
3) 5x²-6x+5=0
a=5 b=-6 c=5
a=5 b=-6 c=5
= (-6)²-4.5.5 = 36-100 = -64
Note que <0 e não existe raiz quadrada de um número negativo. Assim, a equação não possui nenhuma raiz real.
Logo: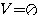 
» vazio
Propriedades
Relações entre coeficientes e raízes
Vamos provar as relações descritas acima:
Dado a equação ax²+bx+c=0, com e , suas raízes são:
A soma das raízes será:
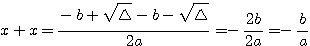
Logo, a soma das raízes de uma equação do 2º grau é dada por:
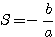
O produto das raízes será:
Logo, o produto das raízes de uma equação do 2º grau é dada por:
Podemos através da equação ax²+bx+c=0, dividir por a.
Obtendo: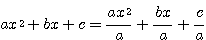 
Substituindo por 
Obtendo a Soma e Produto de uma equação do 2º grau:
x² - Sx + P = 0
Exemplos:
1) Determine a soma e o produto das seguintes equações:
a) x² - 4x + 3=0
Sol] Sendo a=1, b=-4 e c=3:
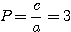
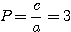
b) 2x² - 6x -8 =0
Sendo a=2, b=-6 e c=-8
c) 4-x² = 0
Sendo a=-1, b=0 e c=4:
Fonte: www.exatas.hpg.ig.com.br
- Takakazu Seki Kowa
ATENÇÃO - tradução automática da versão inglesa Takakazu Seki nasceu em uma família de guerreiros samurais. No entanto, na mais tenra idade ele foi adotado por uma família nobre chamado Seki Gorozayemon. O nome pelo qual é conhecido agora, Seki,...
- A Origem Das Equações Do 1º Grau
François Viète ?Assim como o Sol empalidece as estrelas com o seu brilho, um homem inteligente eclipsa a glória de outro homem nos concursos populares, resolvendo os problemas que este lhe propõe?. François...
- Paul Dirac - Biografia
Paul Dirac (1902 - 1984) Paul Dirac (1902 - 1984) Paul Adrien Maurice Dirac nasceu em, Bristol - Inglaterra a, 8 de Agosto de 1902. Afirmou-se como engenheiro e matemático. Estudou Engenharia elétrica na Universidade de Bristol, completando...
- Equação De 1º Grau
Introdução às equações de primeiro grau Para resolver um problema matemático, quase sempre devemos transformar uma sentença apresentada com palavras em uma sentença que esteja escrita em linguagem matemática. Esta é a parte mais importante e...
- Saindo Da Rotina...
O filho do professor de história estava enchendo o saco do filho do professor de física: - Seu pai é professor de física, é bitolado, doido, só fica resolvendo equação, desenhando esqueminha no quadro-negro, fica olhando raios...