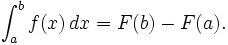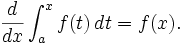Cálculo - Invenções
Calculus é um ramo central da matemática , desenvolvido a partir de álgebra e geometria , e construída em dois grandes idéias complementares.
Um conceito é o cálculo diferencial . Ela estuda as taxas de variação, que geralmente são ilustradas pela encosta de uma linha. Diferencial cálculo baseia-se no problema de encontrar a taxa de variação instantânea de uma quantidade em relação ao outro. Exemplos de problemas típicos de cálculo diferenciais estão encontrando as seguintes quantidades:
- A aceleração e velocidade de um corpo em queda livre em um momento particular.
- A perda na velocidade e trajetória de um projétil disparado, como um projétil de artilharia ou bala.
- Mudar de rentabilidade ao longo do tempo de uma empresa em crescimento em um determinado ponto.
O outro conceito chave é o cálculo integral . Estuda a acumulação de quantidades, como as áreas sob a curva, viagens linear distância ou volume deslocado. Cálculo Integral é o espelho do cálculo diferencial. Exemplos de problemas de cálculo integral incluem encontrar as seguintes quantidades:
- A quantidade de água bombeada por uma bomba com uma potência de entrada set, mas diversas condições de perdas e pressão de bombeamento.
- A quantidade de dinheiro acumulado por uma empresa sob diversas condições de negócios.
- A quantidade de estacionamento arado por um limpa-neve de dado o poder com taxas variáveis ??de queda de neve.
Os dois conceitos, diferenciação e integração, definir operações inversas em um sentido preciso feita pelo teorema fundamental do cálculo . Em ensinar cálculo, pode ser dada qualquer conceito de prioridade. O habitual educacional abordagem é a introdução de cálculo diferencial em primeiro lugar.
História
Embora as origens do cálculo integral são geralmente considerados como não ir mais para trás do que para os gregos antigos , não há evidência de que os antigos egípcios podem ter abrigado tal conhecimento também. (Veja Moscow Mathematical Papyrus .) Eudoxus geralmente é creditado com o método da exaustão , o que tornou possível calcular a área e volume de regiões e sólidos. Archimedes desenvolveu esse método ainda mais, ao mesmo tempo, inventar métodos heurísticos que se assemelham a conceitos modernos. Um matemático indiano, Bhaskara (1114-1185), deu um exemplo do que hoje é chamado de "coeficiente diferencial" ea idéia básica do que é hoje conhecido como "Teorema de Rolle". Leibniz e Newton são normalmente designados os inventores do cálculo, principalmente por suas descobertas separadas do teorema fundamental do cálculo e trabalhar na notação.
Houve um debate considerável sobre se Newton ou Leibniz foi o primeiro a vir para cima com os conceitos importantes do cálculo. A verdade da questão provavelmente nunca será conhecido. A maior contribuição de Leibniz para o cálculo era a sua notação ; muitas vezes ele passou dias tentando chegar com o símbolo apropriado para representar uma idéia matemática. Esta controvérsia entre Leibniz e Newton foi infeliz em que dividiu os matemáticos de língua Inglês daqueles na Europa por muitos anos, a criação de volta análise britânica (ou seja, a matemática à base de cálculo), por um tempo muito longo. Terminologia e notação de Newton era claramente menos flexível do que a de Leibniz, no entanto, foi mantido no uso britânico até o início do século 19, quando o trabalho da Sociedade Analítica viu com sucesso a introdução da notação de Leibniz na Grã-Bretanha. Pensa-se agora que Newton tinha descoberto várias idéias relacionadas ao cálculo mais cedo do que Leibniz tinha; no entanto, Leibniz foi o primeiro a publicar. Hoje, tanto Leibniz e Newton são considerados como tendo descoberto o cálculo de forma independente.
Lesser crédito para o desenvolvimento do cálculo é dado a Barrow , Descartes , de Fermat , Huygens , e Wallis . Um matemático japonês, Kowa Seki , viveram ao mesmo tempo que Leibniz e Newton e também elaborou alguns dos princípios fundamentais do cálculo integral, embora isso não era conhecido no Ocidente, na época, e ele não teve contato com os estudiosos ocidentais. [ 1] (http://www2.gol.com/users/coynerhm/0598rothman.html )
Cálculo diferencial
Ver artigo principal: Derivative
As medidas de derivativos a sensibilidade de uma variável a pequenas mudanças na outra variável. Uma dica é a fórmula:
-
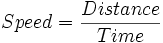para um objeto que se move a uma velocidade constante.
Um de velocidade (um derivado) num carro descreve a mudança na posição relativa para a mudança no tempo. A velocidade em si pode estar mudando; cálculo lida com esta situação mais complexa, mas natural e familiar.
Cálculo diferencial determina a velocidade instantânea , em qualquer dado específico instante no tempo, não apenas a velocidade média durante um intervalo de tempo. A fórmula Velocidade = Distância / Tempo aplicado a um único instante é o quociente sem sentido " de zero dividido por zero ". Isto é evitado, no entanto, porque o quociente distância / tempo não é utilizado para um único instante (ainda que numa fotografia ), mas para os intervalos de tempo que são muito curto.
O derivado responde à pergunta: como o tempo decorrido se aproxima de zero, o que é que a velocidade média calculada pela distância / tempo abordagem ? Em linguagem matemática, este é um exemplo de "tomar um limite . "
Mais formalmente, cálculo diferencial define a taxa de variação instantânea (o derivado ) de uma função matemática 's valor , no que diz respeito às mudanças da variável . O derivado é definido como um limite de um quociente de diferença .
A derivada de uma função fornece informações sobre pequenos pedaços de seu gráfico. Ele é diretamente relevante para encontrar o máximos e mínimos de uma função - porque naqueles pontos do gráfico é plana (ou seja, a inclinação do gráfico é zero). Outra aplicação do cálculo diferencial é o método de Newton , um algoritmo para encontrar zeros de uma função através da aproximação da função por suas tangentes linhas. Cálculo diferencial tem sido aplicada a muitas perguntas que não foram primeiro formuladas na linguagem do cálculo.
O derivado está no cerne das ciências físicas . A lei de Newton do movimento, Força = Massa x Aceleração, tem significado no cálculo porque a aceleração é um derivado. Teoria de Maxwell do eletromagnetismo e da teoria da gravidade de Einstein ( relatividade geral ) também são expressos na linguagem do cálculo diferencial, como é a teoria básica de circuitos elétricos e grande parte da engenharia .
Cálculo Integral
Ver artigo principal: Integral
A integral definida avalia o efeito cumulativo de muitas pequenas mudanças em uma quantidade. O exemplo mais simples é a fórmula
Distância = Velocidade x Tempo
para calcular a distância de um carro move-se durante um período de tempo em que se desloca a constante de velocidade. A distância percorrida é o efeito cumulativo das pequenas distâncias movido em cada um dos muitos segundos o carro está na estrada. O cálculo é capaz de lidar com a situação natural em que o carro se move com a mudança de velocidade.
Cálculo integral determina a distância exata percorrida durante um intervalo de tempo, criando uma série de melhores e melhores aproximações, chamados somas de Riemann , que abordam a distância exata.
Mais formalmente, dizemos que a integral definida de uma função em um intervalo é um limite de Riemann aproximações soma.
Aplicações de cálculo integral surgem sempre que o problema é calcular um número que é, em princípio, (aproximadamente) igual à soma das soluções de muitos problemas e muito menores.
A aplicação geométrica clássico é cálculos da área. Em princípio, a área de uma região pode ser aproximada por cortando-a em muitas quadrados muito pequenos e adicionar as áreas dos referidos quadrados. (Se a região possui um contorno curvo, em seguida, com omissão dos quadrados sobrepostos a bordo não cause demasiado grande erro.) áreas de superfície e volumes também pode ser expressa como integrais definidas.
Muitas das funções que estão integradas são taxas, tal como uma velocidade. Um integrante de uma taxa de variação de uma quantidade em um intervalo de tempo diz o quanto essa quantidade muda durante esse período de tempo. Faz sentido que se alguém conhece a sua velocidade a cada instante no tempo por uma hora (ou seja, eles têm uma equação que relaciona a sua velocidade e tempo), então eles devem ser capazes de descobrir o quão longe eles vão durante essa hora. A integral definida de sua velocidade apresenta um método para fazê-lo.
Muitas das funções que estão integrados representam densidades. Se, por exemplo, a densidade de poluição ao longo de um rio (toneladas por milha) é conhecido em relação à posição, em seguida, o integral de densidade que pode determinar a quantidade de poluição não é em todo o comprimento do rio.
Probabilidade , a base para as estatísticas , é um dos mais importantes aplicações de cálculo integral.
Fundações
O rigoroso fundação de cálculo baseia-se nas noções de função e de um limite ; este último tem uma teoria, em última análise, dependendo de que os números reais como um contínuo . Suas ferramentas incluem técnicas associadas com álgebra elementar , e indução matemática .
O moderno estudo dos fundamentos do cálculo é conhecido como análise real . Isso inclui definições completas e provas de teoremas de cálculo. Ele também fornece generalizações, como a teoria da medida e teoria da distribuição .
Teorema fundamental do cálculo
O teorema fundamental do cálculo afirma que a diferenciação e integração são, em certo sentido, as operações inversas. Mais precisamente, antiderivatives pode ser calculado com integrais definidas, e vice-versa .
Esta ligação permite recuperar a alteração total na uma função ao longo do intervalo de alguns da sua taxa de variação instantânea, integrando este último.
Essa constatação, feita por Newton e Leibniz, foi fundamental para a proliferação massiva de resultados analíticos após a sua obra se tornou conhecido.
O teorema fundamental fornece um método algébrico de computação muitas integrais definidas --sem realizando processos limite - por encontrar fórmulas para antiderivatives . Também é um protótipo de uma solução de equações diferenciais . Equações diferenciais relacionar uma função desconhecida de seus derivados, e são onipresentes nas ciências.
1 st teorema fundamental do Cálculo: Se uma função f é contínua no intervalo [ a , b ] e F é uma antiderivada de f no intervalo [ a , b ], então
2 nd teorema fundamental do Cálculo: Se f é contínua em um intervalo aberto I contendo um , então, para cada x no intervalo,
Aplicações
O desenvolvimento e uso do cálculo teve um alcance amplo efeitos sobre quase todas as áreas da vida moderna. Ela é a base de quase todas as ciências , especialmente física . Praticamente todos os desenvolvimentos modernos, tais como construção técnicas,aviação e outras tecnologias fazer uso fundamental do cálculo. Muitas fórmulas algébricas agora utilizados para balística, aquecimento e refrigeração, e outras ciências práticas foram trabalhados através da utilização de cálculo. Em um manual, uma fórmula algébrica com base em métodos de cálculo pode ser aplicado sem conhecer suas origens.
O sucesso de cálculo foi estendido ao longo do tempo para equações diferenciais , cálculo vetorial , cálculo das variações , análise complexa , e de topologia diferencial .
Ver igualmente
- cálculo com polinômios
- precalculus ( educação )
- lista de tópicos de cálculo
- Importantes publicações em cálculo
- Sistemas Lineares E Determinantes - História
Seki KowaNa matemática ocidental antiga são poucas as aparições de sistemas de equações lineares. No Oriente, contudo, o assunto mereceu atenção bem maior. Com seu gosto especial por diagramas, os chineses representavam os sistemas lineares por...
- Takakazu Seki Kowa
ATENÇÃO - tradução automática da versão inglesa Takakazu Seki nasceu em uma família de guerreiros samurais. No entanto, na mais tenra idade ele foi adotado por uma família nobre chamado Seki Gorozayemon. O nome pelo qual é conhecido agora, Seki,...
- Isaac Newton -- Biografia
Isaac Newton (1642 - 1727) Isaac Newton (1642 - 1727) Físico e matemático inglês Isaac Newton nasceu em 4 de janeiro de 1643 em Woolsthorpe, Inglaterra. Orfão e abandonado pela mãe aos três anos de idade, Newton foi criado pelos avós, tendo...
- Geometria Analítica
ANÁLISE, O QUE É? Com a retomada da geometria grega e o aperfeiçoamento da álgebra, a matemática torna-se cada vez mais essencial para o progresso das demais ciências. Nos séculos XVI e XVII, os avanços da astronomia, as novas questões colocadas...
- Museu Conta História Da Computação
. O Museu de Computação Professor Odelar Leite Linhares, do Instituto de Ciências Matemáticas e de Computação (IMC) da USP São Carlos (a 230 km de São Paulo) concentra velhas máquinas de calcular e os primeiros computadores são algumas das 219...